सामग्री

• पायर्‍या
• टिपा

ज्यांना गणिताची अडचण आहे त्यांच्यासाठी चौरस मूळचे प्रतीक पाहून थंडी थकवा येऊ शकते. तथापि, या ऑपरेटरमध्ये अडचणी येण्यासारख्या कठीण नाहीत. कधीकधी साध्या चौरस मुळांच्या समस्या सोपी गुणाकार किंवा विभागणीइतकीच सोपी असू शकतात. दुसरीकडे, अधिक क्लिष्ट समस्या अधिक काम करू शकतात. तरीही, योग्य पध्दतीसह, ते सर्व सोपे दिसतील. आता चौरस मूळ समस्यांचा सराव करण्यास प्रारंभ करा आणि हे नवीन गणित कौशल्य जाणून घ्या संपूर्ण!

पायर्‍या

3 पैकी भाग 1: चौरस आणि चौरस मुळांची संकल्पना समजून घ्या

1. 

   चौरस मुळे समजण्यापूर्वी प्रथम संख्येचा वर्ग म्हणजे काय हे समजून घ्या. हे समजणे सोपे आहे. संख्येचे वर्ग काढण्यासाठी, त्यास स्वतःच गुणाकार करा. उदाहरणार्थ, 3 चौरस 3 = 3 = 9 सारखेच आहेत आणि 9 चौरस 9 × 9 = 81 प्रमाणेच आहेत. वर्ग वाढवल्या जाणार्‍या संख्येच्या वरच्या उजव्या बाजूला असलेल्या "2" ने दर्शविले आहेत, हे जसे: 3, 9, 100 इत्यादी.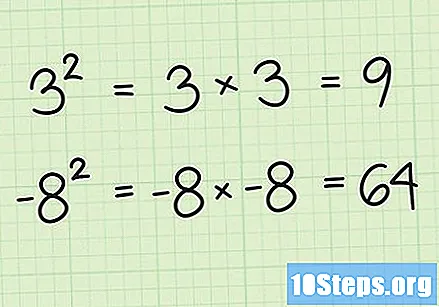
   • संकल्पनेचा सराव करण्यासाठी, आणखी काही संख्या वर्गित करण्याचा प्रयत्न करा. लक्षात ठेवा, संख्या वर्गीकरण करणे केवळ स्वतःच गुणाकार करीत आहे. आपण हे नकारात्मक संख्यांसह देखील करू शकता परंतु लक्षात ठेवा की या प्रकरणात उत्तर नेहमीच सकारात्मक असेल. उदाहरणार्थ, -8 = -8. -8 = 64.

2. 

   
   
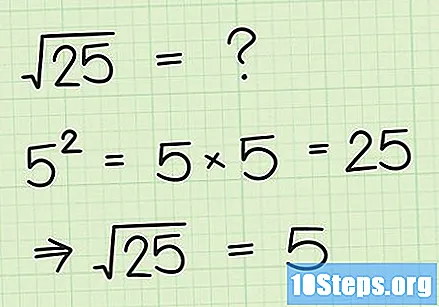
   चौरस मूळ शोधण्यासाठी, क्षमतेचा "व्यस्त" शोधा. मूळ चिन्ह (√, ज्याला "रॅडिकल" देखील म्हटले जाते) याचा अर्थ मुळात चिन्हाचा "विरुद्ध" असतो. जेव्हा आपण मूलगामी पाहता तेव्हा स्वत: ला विचारा, “मी स्वतःच किती संख्या गुणाकार करू शकेन की परिणामी संपूर्ण क्रांतीमधील संख्या येईल?” उदाहरणार्थ, जेव्हा आपण √ (9) पाहता तेव्हा वर्गित संख्या शोधण्याचा प्रयत्न करा, नऊ बरोबरीचे. या प्रकरणात उत्तर मिळेल तीनकारण 3 = 9.
   • दुसरे उदाहरणः 25 (√ (25)) चा वर्गमूल शोधू. याचा अर्थ असा की आपल्यास चौरस असलेली संख्या 25 असणे आवश्यक आहे. 5 = 5 × 5 = 25 असल्याने आपण असे म्हणू शकतो की √ (25) = 5.
   • आपण या ऑपरेशनचा स्क्वेअर एलिव्हेशन "पूर्ववत" करण्याच्या मार्गाचा विचार करू शकता. उदाहरणार्थ, जर आपल्याला 64 (root,), the root चा वर्गमूल शोधण्याची गरज असेल तर आपण as 64 इतका 8. असा विचार केला पाहिजे कारण स्क्वेअर रूट मुळात एक उंची चौरस "रद्द करते" म्हणून आपण असे म्हणू शकतो की √ () 64) = √ ()) = 8.

3. 

   
   
   परिपूर्ण चौरस संख्या आणि अपूर्ण चौरस संख्यांमधील फरक समजून घ्या. आतापर्यंत आमच्या चौरस समस्यांच्या उत्तरांची पूर्ण संख्या आहे. हे नेहमीच होणार नाही. खरं तर, रेडिएशन ऑपरेशनचा परिणाम कधीकधी लांबलचक, गुंतागुंतीचा दशांश होऊ शकतो. जर संख्येचे मूळ एक पूर्णांक असेल, म्हणजेच ते अपूर्णांक किंवा दशांश नसल्यास, त्यास म्हटले जाईल परिपूर्ण स्क्वेअर. वर दर्शविलेली सर्व उदाहरणे (9, 25 आणि 64) परिपूर्ण वर्ग आहेत कारण त्यांची मुळे पूर्णांक आहेत (अनुक्रमे 3, 5 आणि 8,)
   • दुसरीकडे, ज्यांची मुळे पूर्ण नाहीत अशा संख्येस म्हटले जाते अपूर्ण वर्ग. यापैकी एका संख्येच्या मूळची गणना करताना आम्हाला एक परिणाम मिळेल जो सामान्यत: भाग किंवा दशांश असेल. कधीकधी, यात समाविष्ट दशांश खूप जटिल असू शकतात, उदाहरणार्थ: √ (13) = 3,605551275464...

4. 

   
   
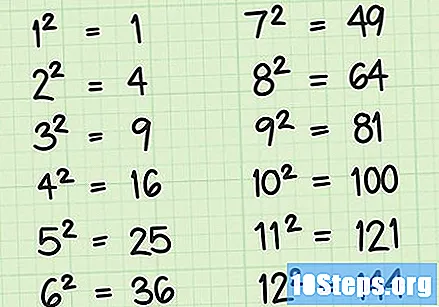
   कमीतकमी प्रथम 12 परिपूर्ण स्क्वेअर लक्षात ठेवा. जसे आपण दर्शवितो, संख्येच्या वर्गमूलची गणना करणे खूप सोपे आहे! म्हणून प्रथम डझन परिपूर्ण चौरसांच्या चौरस मुळे लक्षात ठेवण्यासाठी वेळ घेणे आवश्यक आहे. चाचण्यांवर त्यांचा बराचसा कल असतो, म्हणून त्यांचे स्मरण केल्याने आपला बराच वेळ वाचू शकेल. प्रथम 12 परिपूर्ण वर्ग हे आहेत:
   • 1 = 1 × 1 = 1
   • 2 = 2 × 2 = 4
   • 3 = 3 × 3 = 9
   • 4 = 4 × 4 = 16
   • 5 = 5 × 5 = 25
   • 6 = 6 × 6 = 36
   • 7 = 7 × 7 = 49
   • 8 = 8 × 8 = 64
   • 9 = 9 × 9 = 81
   • 10 = 10 × 10 = 100
   • 11 = 11 × 11 = 121
   • 12 = 12 × 12 = 144

5. 

   शक्य असल्यास, परिपूर्ण चौरस काढून मुळे सुलभ करा. अपूर्ण स्क्वेअरचे स्क्वेअर रूट शोधणे खूप अवघड आहे, विशेषत: जर तेथे कोणतेही कॅल्क्युलेटर उपलब्ध नसेल (खालील विभागांमध्ये आपण प्रक्रिया सुलभ करण्यासाठी युक्त्या शिकू शकता). तथापि, गणना करणे अधिक सुलभ करण्यासाठी कधीकधी मूळच्या आत संख्या सुलभ करणे शक्य होते. फक्त मुळांच्या आतील भागास घटकांमध्ये विभागून नंतर परिपूर्ण चौरस असलेल्या घटकांच्या मुळाची गणना करा आणि मूलगामीच्या बाहेर उत्तर लिहा. हे जे दिसते त्यापेक्षा सोपे आहे. अधिक चांगले समजण्यासाठी खाली पहा!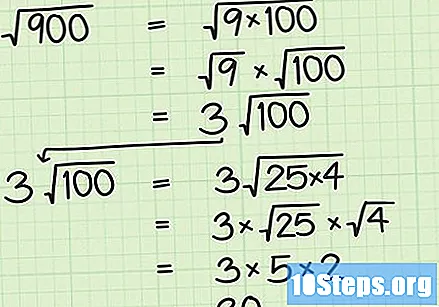
   • समजा आपल्याला 900 चे मूळ शोधणे आवश्यक आहे. सुरुवातीला हे एक कठीण काम असल्याचे दिसते! जर 900 मध्ये घटकांमध्ये विभागले तर सर्व काही अधिक सोपे आहे. “X” संख्येचे घटक म्हणजे संख्यांचा संच असतो, जर गुणाकार केला तर त्याचा परिणाम “x” होईल. उदाहरणार्थ, 1 × 6 आणि 2 × 3 गुणाकार करून आपण 6 मिळवू शकतो, म्हणून 6 चे घटक 1, 2, 3 आणि 6 आहेत.
   • 900 सह कार्य करण्याऐवजी जे थोडेसे विचित्र होऊ शकते, त्याऐवजी ते 9 × 100 असे लिहा. आता 9, जे परिपूर्ण चौरस आहे, 100 पासून विभक्त झाले आहेत, आम्ही त्याचे वर्गमूळ मोजू शकतो. √ (9 × 100) = √ (9) × √ (100) = 3 × √ (100) म्हणजेच, √ (900) = 3√(100).
   • १०० ला २ times आणि into मध्ये विभागून आम्ही अजून दोन वेळा सुलभ करू शकतो. √ (१००) = √ (२× × ×) = √ (२ 25) × √ ()) = × × २ = १०. तर, आम्ही असे म्हणू शकतो की √ (900) = 3 (10) = 30.

6. 

   नकारात्मक संख्येच्या मुळाची गणना करण्यासाठी काल्पनिक संख्या वापरा. स्वत: ला विचारा, -१ in मध्ये स्वतः कोणत्या गुणाकाराचा परिणाम होतो? हे 4 किंवा -4 नाही, कारण या दोन संख्यांचा वर्ग 16 आहे. आपण सोडून द्यावे? खरं तर, फक्त वास्तविक संख्या वापरुन -16 किंवा इतर कोणतीही नकारात्मक संख्या लिहिण्याचा कोणताही मार्ग नाही. अशा परिस्थितीत, नकारात्मक संख्येचा वर्ग मूळ बदलण्यासाठी आपण काल्पनिक संख्या (सहसा अक्षरे किंवा चिन्हे स्वरूपात) वापरली पाहिजेत. उदाहरणार्थ "i" व्हेरिएबल -1 चा वर्गमूल दर्शविण्यासाठी वापरला जातो. सामान्य नियम म्हणून, नकारात्मक संख्येचे मूळ नेहमीच एक काल्पनिक संख्या असेल (किंवा कमीतकमी समाविष्ट करा).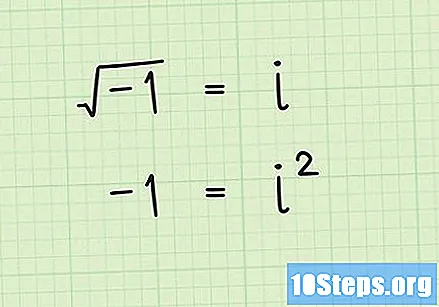
   • लक्षात ठेवा, काल्पनिक संख्या वास्तविक संख्यांद्वारे दर्शविली जाऊ शकत नाहीत तरीही, त्यांना काही मार्गांनी अशा प्रकारे मानले जाऊ शकते. उदाहरणार्थ, “-x” नकारात्मक क्रमांकाचे मूळ जर वर्ग केले तर त्याचा परिणाम इतर मुळांप्रमाणेच “-x” मध्येही होतो. म्हणजेच, i = -1

भाग 3 चा 2: लांब विभाग-सारख्या पद्धती वापरणे

1. 

   स्क्वेअर रूट समस्येवर असे उपचार करा की जणू ती लांब विभाग आहे. थोड्या कष्टकरी असूनही, आपण कॅल्क्युलेटर न वापरता क्लिष्ट अपूर्ण चौरस संख्यांचा वर्गमूल शोधू शकता. पद्धत (किंवा अल्गोरिदम) लांब प्रभावाप्रमाणेच आहे (परंतु समान नाही). लांब विभाग म्हणजे पारंपारिक पद्धत हाताने विभागांची गणना करण्यासाठी वापरली जाते.
   • समस्येच्या प्रारंभिक स्थितीसह प्रारंभ करा, जे लांब प्रभागांसारखेच असेल. उदाहरणार्थ, असे म्हणूया की आपल्याला 6.45 चे मूळ शोधण्याची आवश्यकता आहे, जे निश्चितपणे परिपूर्ण वर्ग नाही. प्रथम आपण एक स्क्वेअर रूट चिन्ह (√) लिहितो आणि नंतर त्यात आपला क्रमांक ठेवतो. मग, चिन्हापासून एक ओळ तयार करणे आवश्यक आहे - जोपर्यंत ती संपूर्ण संख्या कव्हर करेपर्यंत, बॉक्सच्या आत सोडत नाही जिथे लांब विभाग विभाजक आहे. फरक इतका आहे की येथे उत्तर पारंपारिक विभाग प्रमाणे त्या बॉक्सच्या खाली नसून त्या खाली असेल. जेव्हा आपण समाप्त कराल, तेव्हा आपल्याकडे संपूर्ण "6.45" संख्येसह विस्तृत "sign" चिन्ह असेल.
   • या बॉक्स वर क्रमांक लिहा, मग जागा सोडा.

2. 

   अंक जोडीमध्ये गटबद्ध करा. समस्येचे निराकरण करण्यास, दशांश बिंदूपासून प्रारंभ करून, स्टेमच्या आत अंकांचे अंक जोडीमध्ये जोडा. जोड्या वेगळे करण्यासाठी आपण लहान चिन्हे (जसे की पूर्णविराम, बार, स्वल्पविराम इ.) तयार करू शकता.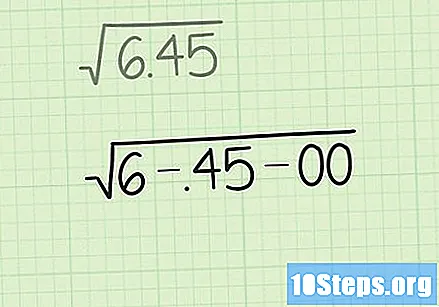
   • आमच्या उदाहरणात, आम्ही याप्रमाणे 6.45 ला तीन जोड्यांमध्ये विभागले पाहिजे: 6-,45-00. डाव्या बाजूला एक कमी अंक आहे हे पहा, त्यात कोणतीही अडचण नाही.

3. 

   प्रथम "गटा" च्या मूल्यापेक्षा कमी किंवा त्या समान चौरस असलेली सर्वात मोठी संख्या शोधा. डाव्या बाजूला पहिल्या जोड्यांसह प्रारंभ करा. सर्वात मोठा संख्या निवडा ज्याचा वर्ग "समूहा" पेक्षा कमी किंवा समान असेल. उदाहरणार्थ, गट was 37 असेल तर choose निवडा, कारण = = <<<this but पण = =>> 37 37. पहिल्या गटाच्या वर हा क्रमांक लिहा. हा उत्तराचा पहिला अंक आहे.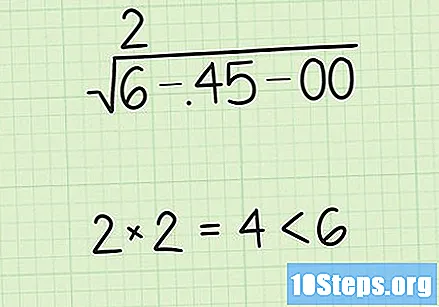
   • आमच्या उदाहरणात, 6-, 45-00 मधील प्रथम गट 6 आहे. प्रथम सर्वात मोठी संख्या ज्याचा वर्ग 6 पेक्षा कमी किंवा समान आहे 2, कारण 2 = 4. रॅडिकल मध्ये असलेल्या 6 वर "2" लिहा.

4. 

   उत्तराचा पहिला अंक पहा (आम्हाला आत्ताच सापडलेली संख्या) आणि त्यास दोनने गुणाकार करा. आता पहिल्या गटाच्या खाली निकाल लिहा आणि फरक शोधण्यासाठी वजाबाकी करा. त्यानंतर, पुढील नंबरची जोडी खाली स्क्रोल करा आणि त्यामध्ये आम्हाला आढळलेल्या फरकामध्ये जोडा. शेवटी, शेवटचा अंक डाव्या बाजूला उत्तराचा पहिला अंक दुप्पट लिहा आणि त्याच्या बाजूला एक जागा सोडा.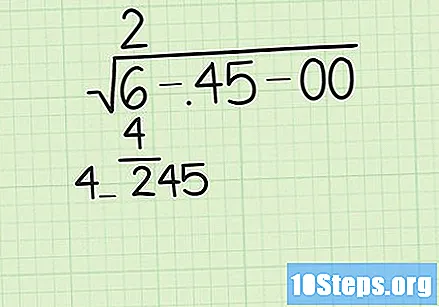
   • आमच्या उदाहरणात, पहिली पायरी 2 ची दुप्पट शोधणे असेल जे उत्तराचा पहिला अंक आहे. २ × २ = Then. त्यानंतर, आम्ही उत्तर म्हणून २ मिळविते 6 वरून (आमच्या प्रथम "गट") वजा करणे आवश्यक आहे. 245 मिळविण्यासाठी आता आपल्याला पुढच्या गटामध्ये जाणे आवश्यक आहे (45). शेवटी, आम्ही डावीकडे पुन्हा 4 लिहितो, उजवीकडील एक छोटीशी रिक्त जागा ठेवून, 4_.

5. 

   रिकाम्या जागा भरा. आता आपल्याला डाव्या बाजूला लिहिलेल्या नंबरच्या पुढे रिक्त जागेच्या जागी अंक ठेवणे आवश्यक आहे. तो अंक निवडा, जेव्हा डावीकडील रिक्त जागेसह स्वतःस पुनर्स्थित केल्याने गुणाकार केला तर अधिकतम मूल्य असेल, परंतु उजवीकडील संख्येपेक्षा कमी असेल. हे थोडेसे क्लिष्ट वाटू शकते, म्हणून समजून घेण्यासाठी काही उदाहरणे पाहूया. खाली गेलेली संख्या, म्हणजेच, उजवीकडील एक संख्या 1700 आणि उजवीकडील संख्या 40_ असेल तर आम्ही 4 नंबरसह रिक्त जागा भरू कारण 404 × 4 = 1616 <1700 आणि 405 × = 2025 या चरणात सापडलेली संख्या उत्तराचा दुसरा अंक असेल, तर आपण ते स्टेम चिन्हाच्या वर जोडू शकता.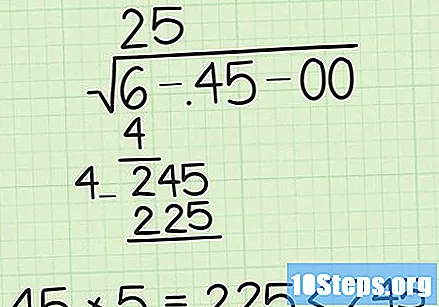
   • आमच्या उदाहरणात, आम्हाला रिक्त जागा भरण्यासाठी संख्या शोधणे आवश्यक आहे 4_ × _ जे उत्तर शक्य तितके मोठे करते, परंतु 245 च्या तुलनेत किंवा त्यापेक्षा कमी आहे. आमच्या बाबतीत उत्तर आहे 5कारण 45 × 5 = 225 आणि 46 × 6 = 276.

6. 

   उत्तर लिहिण्यासाठी रिक्त स्थान भरलेल्या संख्या वापरणे सुरू ठेवा. रॅडिकलमधून खाली येणा number्या संख्येचे वजा करुन किंवा आपण इच्छितेपर्यंत अचूकतेपर्यंत पोहोचत नाही तोपर्यंत ही सुधारित लांब विभाग पद्धत सुरू ठेवा. पूर्ण झाल्यावर, प्रत्येक चरणात रिक्त जागा भरण्यासाठी वापरल्या जाणार्‍या नंबर (आणि अर्थातच आम्ही वापरत असलेली पहिली संख्या) उत्तर अंक बनवेल.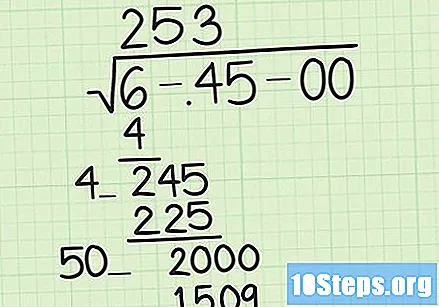
   • आमचे उदाहरण पुढे ठेवून आम्ही २० get मिळवण्यासाठी २ 245 वरून २२5 वजा करू. त्यानंतर २००० मिळवण्यासाठी आम्ही 00 च्या अंकांची जोडी खाली जाऊ. मूलगामीच्या वरील संख्येच्या दुप्पटतेने आपल्याकडे 25 × 2 = 50 आहे. रिक्त संख्या सेट करून 50_ setting _ = / <2,000, आम्हाला मिळेल 3. या क्षणी, आमच्याकडे मूलगामीबद्दल "253" आहे. प्रक्रियेची पुन्हा पुनरावृत्ती केल्यावर आम्हाला पुढील अंकांप्रमाणे 9 मिळेल.

7. 

   उत्तरामध्ये स्वल्पविराम योग्य स्थितीत ठेवा. उत्तर पूर्ण करण्यासाठी, आम्हाला अद्याप दशांश बिंदू योग्य ठिकाणी ठेवणे आवश्यक आहे. हा भाग सुलभ आहे: फक्त उत्तरामध्ये स्वल्पविरामात त्याच स्वरूपाच्या स्वल्पविरामात कॉमा द्या. उदाहरणार्थ, जर रॅडिकलच्या आतील क्रमांक 49.8 असेल तर खाली असलेल्या प्रमाणेच उत्तरेमध्ये स्वल्पविराम द्या, म्हणजेच 9 आणि 8 वरील दोन संख्यांच्या दरम्यान.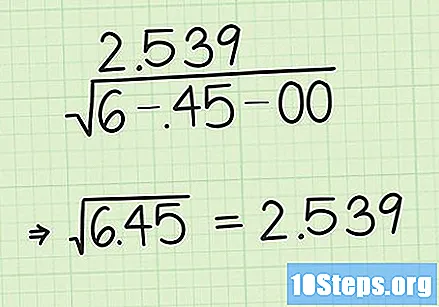
   • आमच्या उदाहरणात, मूलगामी अंतर्गत संख्या 6.45 आहे. उत्तर मिळविण्यासाठी, उत्तर मिळविण्यासाठी फक्त and आणि above च्या वरच्या संख्येच्या दरम्यान स्वल्पविराम ठेवा, जे या प्रकरणात उत्तर मिळवण्यासाठी अनुक्रमे २ आणि are आहेत: 2,539.

भाग 3 चे 3: अपूर्ण चौकांचे द्रुतपणे अनुमान काढणे

1. 

   एका अंदाजानुसार उत्तर शोधा. एकदा आपल्याला काही परिपूर्ण चौकांचे मूळ माहित झाल्यास, अपूर्ण चौकांचे मूळ शोधणे खूप सोपे होईल. मागील चरणात, आम्ही कमीतकमी पहिले बारा परिपूर्ण वर्ग आणि त्यांची मुळे लक्षात ठेवण्याची शिफारस करतो. चांगली बातमी अशी आहे की आम्ही परिचित असलेल्या चौरसांच्या मुळाचे अंदाजे अनुमान काढण्यासाठी वापरू शकतो जे आपल्याला माहित असलेल्या दोन परिपूर्ण वर्गांच्या दरम्यान आहे. त्यासाठी, आम्हाला अपेक्षित संख्येपेक्षा पहिला परिपूर्ण चौरस आणि शेवटचा लहान एक शोधणे आवश्यक आहे जेणेकरून प्रश्नांची संख्या त्या दोघांमधील असेल. मग, या दोन परिपूर्ण वर्गांपैकी कोणत्यापैकी अपेक्षित संख्येचे मूळ सर्वात जवळ आहे हे शोधण्याचा प्रयत्न केला पाहिजे.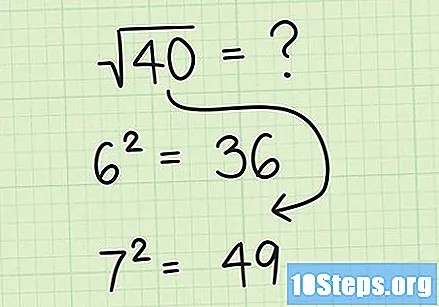
   • उदाहरणार्थ, समजा आपल्याला of० चा वर्गमूल शोधणे आवश्यक आहे. आपण आपले परिपूर्ण चौरस लक्षात घेतल्यामुळे असे म्हणू शकतो की is० हे and ते between दरम्यान म्हणजेच 36 36 आणि between between च्या दरम्यान आहे. 40 हे than पेक्षा मोठे असल्यामुळे त्याचे वर्गमूल असेल. 6.. पेक्षा जास्त तसेच, त्याचे मूळ than पेक्षा कमी असल्याने, त्याचे मूळ than. पेक्षा कमी असेल. 49 than than than पेक्षा 36 36 च्या अगदी जवळ आहे, तर आपले उत्तर कदाचित पुढच्या चरणांमध्ये 6. च्या जवळ असेल. , आम्ही आमच्या अंदाजाची अचूकता वाढवू.

2. 

   एका दशांश ठिकाणी सुस्पष्टता वाढवा. एकदा आपणास आपली संख्या असलेल्या श्रेणीचे दोन सलग परिपूर्ण स्क्वेअर सापडल्यानंतर, अंदाजाची अचूकता केवळ त्या बिंदूपर्यंत वाढवण्याचा प्रयत्न करा ज्यास आपण समाधानकारक वाटता. अंदाज सुधारण्यासाठी जितके अधिक प्रयत्न केले जातील तितके अचूकता. सुरू करण्यासाठी, प्रथम दशांश स्थानाचे मूल्य अनुमान लावा. हा अंदाज बरोबर असणे आवश्यक नाही, परंतु उत्तराच्या अगदी जवळील असू शकेल असे मूल्य निवडण्यासाठी तर्कशास्त्र वापरल्याने प्रक्रिया सुलभ होईल.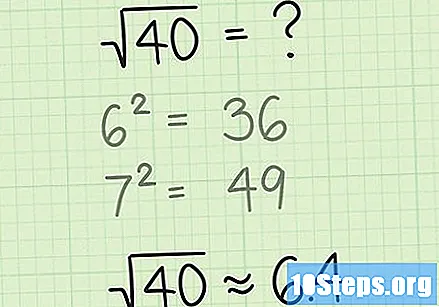
   • आमच्या उदाहरणात, 40 च्या चौरस मुळासाठी एक स्वीकार्य अंदाज असू शकतो 6,4, कारण आम्हाला आधीच माहित आहे की उत्तर कदाचित 7 पेक्षा 6 च्या अगदी जवळ आहे.

3. 

   अंदाज स्वतःच गुणाकार करा. आपण फार भाग्यवान नसल्यास परिणाम प्रारंभ होणारी संख्या (40, आमच्या उदाहरणात) होणार नाही. अचूक उत्तराच्या जवळ जाण्यासाठी आपल्याला अंदाज समायोजित करण्याची आवश्यकता असेल.जर निकाल सुरुवातीच्या संख्येपेक्षा जास्त असेल (म्हणजेच 40 च्या वर), कमी अंदाज करून पहा. त्याचप्रमाणे निकाल अपेक्षित संख्येपेक्षा कमी असल्यास अंदाज वाढवा.
   • 6.4 × 6.4 = मिळविण्यासाठी 6.4 स्वतः गुणा 40,96जो आमच्या आरंभिक संख्येपेक्षा किंचित जास्त आहे.
   • आता, आमचा अंदाज अगदी बरोबर मूल्यापेक्षा वरचढ आहे, म्हणून आपण त्यामध्ये दशांश कमी करू आणि 6.3 × 6.3 = 39,69. आता निकाल आमच्या मूळ संख्येपेक्षा थोडा कमी लागला होता. याचा अर्थ असा की 40 ची मूळ काही संख्या आहे 6.3 आणि 6.4 दरम्यान. शिवाय, 39.69 40.96 पेक्षा 40 च्या जवळ असल्याने, आपल्याला माहित आहे की मूळ 6.4 च्या जवळपास 6.3 च्या जवळ असेल.

4. 

   आवश्यक असल्यास अंदाज सुधारणे सुरू ठेवा. याक्षणी, जर आपण उत्तराशी समाधानी असाल तर, अंदाज म्हणून प्रथम अंदाजे एक वापरा. तथापि, आपल्याला अधिक अचूक उत्तराची आवश्यकता असल्यास, फक्त याचा अंदाज करण्याचा प्रयत्न करा दुसरे दशांश स्थानमागील दोन (म्हणजेच 6.3 आणि 6.4 मधील) दरम्यान मूल्य निवडणे. या पद्धतीचा वापर करून, आम्ही केवळ उत्तरासाठी आवश्यक सुस्पष्टतेवर अवलंबून तीन दशांश ठिकाणांचा अंदाज लावू शकतो.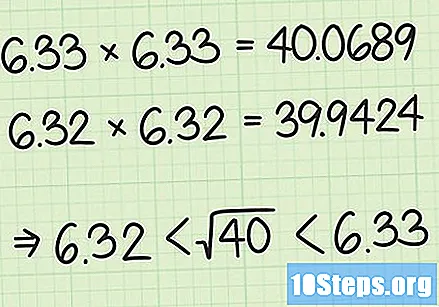
   • आमच्या उदाहरणात, आम्ही आपला अंदाज दोन दशांश ठिकाणी 6.33 निवडू शकतो. 6.33 × 6.33 = 40.0689 प्राप्त करण्यासाठी स्वतःच 6.33 गुणाकार करा. हा निकाल आमच्या आरंभिक संख्येपेक्षा थोडा जास्त असल्याने आम्ही 6.32 सारख्या किंचित कमी किंमतीची निवड करू शकतो. या प्रकरणात, 6.32 × 6.32 = 39.9424, प्रारंभ संख्यापेक्षा थोडे कमी परिणाम. म्हणूनच आम्ही निष्कर्ष काढू शकतो की 40 ची वास्तविक मुळ आहे 6.32 आणि 6.33 दरम्यान. आवश्यक असल्यास, आम्ही आवश्यक संख्येच्या मुळाशी वाढत्या अचूक अंदाजे मिळविण्यासाठी ही पद्धत चालू ठेवू शकतो.

टिपा

• आपल्याला द्रुत निराकरण आवश्यक असल्यास, कॅल्क्युलेटर वापरा. बरेच आधुनिक कॅल्क्युलेटर त्वरित चौरस मुळे मोजू शकतात. सर्वसाधारणपणे, फक्त कोणतीही संख्या टाइप करा आणि स्क्वेअर रूट चिन्हासह बटण दाबा. 1 84१ चे मूळ शोधण्यासाठी, उदाहरणार्थ, उत्तर मिळवण्यासाठी फक्त 8, 4, 1 आणि नंतर (√) दाबाः 39.